
はじめに
先日から、当blog界隈で確率・統計が話題になっている。
発端は、「mixi のコミュニティ一覧がウザい日」という記事。
いきさつを簡単に説明する。
僕は mixi で44個のコミュニティに参加している。
そのうち、7つは「ちりとてちん」の登場人物に関するものである(以下「底抜けコミュ」と呼ぶ)。
さて、mixi のトップページには、自分の参加しているコミュニティの中から、9個が選ばれてリストアップされる
このとき、「底抜けコミュ」7つが全て選ばれる確率はどの程度か。
※なお、実際の mixi のコミュニティ選択アルゴリズムは、ランダムではないことがわかっている。理論上の数値よりも、かなり高い確率で7つが勢揃いするようになっている。
解答への挑戦 (数式編)
この問題を解くためには、「順列」と「組み合わせ」の概念を使えば良いことは想像がつく。
しかし、僕にはそれを使いこなすだけの能力が備わっていない。
初めに僕は、
1/44!/(44-7)!
などという、トンマな計算をやってる。
どうしてそうなるかの説明もないし、今となっては自分でも理解できない。
さて、そんな僕を見て、何人かの読者がこの問題にチャレンジしてくれた。
sterai 説
「7個の『底抜けコミュ』から7個取り出す組合せ」×「37個の『その他のコミュ』から2個取り出す組合せ」×それら9つのコミュの並べ方(順列)÷全ての並べ方、つまり、7C7×(44-7)C2×9P9÷44P9、ではないかと考えました。エクセルで計算すると、0.0001%くらいかと。
大彦説
全部で44のコミュニティがあって、そのうち表示されるコミュニティが9つあるのだから、全ての組合せは44P9ですね。で、7つは底抜けコミュで、2つはその他のコミュなわけね。2つのコミュが9つのいずれかに入る順列は9C2で、残りの42コミュから7つのコミュが取り出される組合せは 42P7だから、
9C2×42P7÷44P9≒0.019
じゃね? およそ2%の確率。
どっちも正しそうに見える。ただし、両者の確率の間にはなんと2万倍の開きがある。例えば、1日1回ずつトップページに配置されるコミュニティのアイコンがシャッフルされるとしよう。このとき、大彦説(2%)をとれば、年間に7日ほどは「底抜けコミュ」が7つ揃うことになる。しかし、sterai 説をとると、2740年に1度しかそういうことは起きない計算になる。
まったく意味が違う!
少なくとも一方は計算がおかしいのだろうなと思う。
#場合によっては、二人とも間違っているかもしれない。
もし、理路整然と正しい確率を説明できる人がいたら、ぜひ教えてください。
解答への挑戦 (シミュレーション)
ところで、sterai さんが「シミュレーションやりゃいいんじゃね?」みたいなことを言っていた。
そういうわけで、チラッとやってみた。
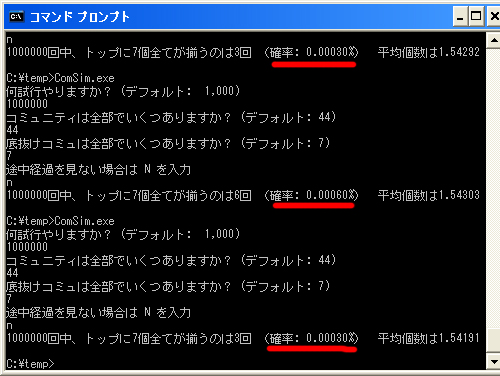
結論から述べる。僕のシミュレーション結果では、7つの「底抜け」コミュが全てトップに表示される確率は、およそ 0.0003%(多少誤差はある)。
100万回の並び替えを行っても、たった3回しか発生しなかった。毎日並び替えを行うと、約1000年に1度しか発生しない確率だ。
大彦説よりも、sterai説の方がはるかに近い。細かい値は一致しないが、誤差とみなしていいかもしれない。実際、写真でみても、3回のうち1回は 0.0006% という値が出てるなど安定しない。ただ、どう考えてもものすごく小さい確率であることには間違いがなさそうだ。
ちなみに、今回作ったVBプログラムのソース (VisualBasic)と実行ファイル(ComSim.exe)(要 .NET 環境。最近のWindows 環境なら普通に動くだろう)を置いておくので、点検したい方はどうぞ。
プログラムの利用方法
コマンドプロンプトで実行してください。
初めに、条件設定についていくつか質問されるので、キーボードで入力して Enter キーを押してください。
考えるのがめんどくさい人は、Enter を押しまくれば、初期値のまま動きます。
なお、ほとんどエラーチェックは入れてないので、紳士的に、半角英数字を使って値を入力してください。
1. 「何試行やりますか?」
試行数を増やすほど、信用できる結果が得られます。ただし、試行数を増やすと、結果が出るまでに時間がかかります。まずは、デフォルトの1,000回で様子を見て、コンピュータに余裕がありそうなら、徐々に増やしてください。
2. 「コミュニティは全部でいくつありますか?」
聞かれたとおりです。初期値は、僕の実際の mixi コミュニティ数にあわせて、44にしてあります。
3. 「底抜けコミュは全部でいくつありますか?」
聞かれたとおりです。「底抜けコミュ」とか言わなくてもいいのですが、僕の実際の mixi コミュニティにあわせてそういう表現にしました。初期値は、これまた実際にあわせて 7です。
4. 「途中結果を見ない場合はNを入力」
超お薦め機能。
100万回の試行数だって、10秒くらいで終わる!(ウチでは途中結果を見ると、15分くらいかかった)
#やっぱさぁ、画面表示って時間がかかるんだよねぇ。
結果の見方(途中経過)
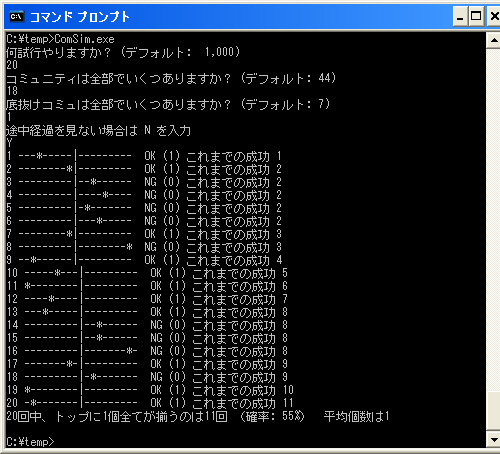
画面表示をありにすると、途中経過を見ることができます。ちゃんとシャッフルされてるかどうかも確認できます。
左から順に
・試行数
・コミュニティをランダムに並べた結果
アスタリスクは「底抜け」コミュ、ハイフンはそれ以外を表す
左から9つのスロットを mixi のトップページとみなしている(タテ線で区切りを入れてある)
・OK: 7つ全てがトップに並んだ、NG: そうならなかった
括弧内の数字は、トップページにアスタリスクが何個あるか
・これまでの試行で、何回OKが出たか
そして、最後の行には結果のサマリーを載せている。
プログラムがあっているか調べるために、いくつか条件を変えて調べた。まぁ、直感に反しない結果が得られることは確認した。
例えば、18個のコミュに入っていて、「底抜けコミュ」が1つだけの場合を考える(上の図)。スロットが18個あり、それはトップ掲載分のちょうど倍。ということは、たった1つの「底抜けコミュ」がトップに出るか否かは半々の確率。上の図ではおよそ50%になってるし、途中経過(20試行)も正しい。
プログラムのロジックに関して
プログラムでは、VisualBasic 標準の擬似乱数関数を使っているので、厳密なランダムが行われているとはいえない。しかし、まぁ、許容範囲だと思ってください。人の命や財産が関わるプログラムじゃないし、学術論文でもないし。つーか、僕の馴染みのある業界だと、どんな乱数の関数を使ったかなんて誰も気にしないし。
あと、コミュニティをシャッフルする時に使ったロジックも甘いかもしれない。配列を上から順番になめて行って、(自分自身を含めた)他のランダムな配列と入れ替えるというやり方。このやり方、別にそんなに悪くないんだよね?(証明とかは知らないし、もっと良いやりかたっつーのも知らないが)
というわけで、「順列」と「組み合わせ」を使って手で計算するだけの能力のない当方。某TK氏が言うところの、「貧者の数学」=コンピュータ・シミュレーションで計算してみました。
繰り返しになりますが、ちゃんと手で解ける賢い人、バシッと解いてください。
お願いします。
strai さんの考え方が正しい。ただ、式ではC(組み合わせ)とP(順列)が混在しているので、Cだけで表現したほうがよろし。
つまり、{7C7 * (44-7)C2} / 44C7
nCn = 1 なので、sterai 式の最初の項に意味がないように思えて、その思い込みから「きっと間違ってる」と思っていたのですが。
今、もう一度考え直して、腑に落ちました。
まず、説明の一貫性のため、たとえ 1 であっても 7C7 はあってもよいと思うようになりました。
そして、次に気づいたことが重要なんだと思うけれど、ようするに、「底抜け以外のコミュニティから、ちょうど2個*だけ*が選ばれる状況」を考えればいいんですね。その場合の数が (44-7)C2 だ。
それを、全体の場合の数 44C7 で割るわけか。なるほどぉ。
どこのどなたか存じませんが、どうもありがとうございます。
ちょっと待った。匿名さんの分母の “44C7” はこれでいいんだっけ?
44C9 の typo?
分母は、44個のコミュから9個を選んだ数だと思うから、44C9 だと思うのだけれども。
プログラム見ました。コメント部分が文字化けしちゃってて、sumCountが何を示す変数なのかちょっとよくわからなかったんですけど、2つ目の画像の例(20回繰り返し、底抜け1個、他17個)で、平均個数が0.55個(11個÷20回繰り返し)にならないのは何でなんでしょうか?
44P9 / 9P9 = 44C9ですから、たぶん44C9でしょうね。
というわけで、
{7C7 * (44-7)C2} / 44C9
が決定版ですかね。
順列と組合せが混在していて、そこから抜け出せなかったところが僕の限界ですね。と言うか、最初に思いついたのが、分母の44P9だったので、分子も順列ベースにあわせるしかなかった(涙)。
あ、しつれい。44C9 のうちまつがいですた。
steraiさん:
ソースの文字化けは、ブラウザで見るとダメみたい。ダウンロードしてテキストエディタ等で開くとどうですか?
最後の平均個数が0.55にならないのは、なんかおかしいですね。Interger に丸められたせいかと思ったけれど、それだったら「確率」のところも丸められるはずだし。
うーむ。
匿名さん:
高名の木登りかな?:p
って、画像みたら「確率」のところも丸まってるじゃん!
普通の人には丸まってるように見えなくても、俺には丸まってる。
理由がわかった。
これは、バグじゃなくて仕様だ。
試行回数に応じて、有効桁数を変化させるという小賢しいプログラムになってるんです。
小数点以下が、{log10(試行回数)-1} とかになるようにしたんだと思う。写真の例だと、試行回数が20回で少なすぎるから、小数点以下は出ないようになってます。それで、平均個数が1に丸められたのです。
プログラムを作り初めてすぐに、どうも百万のオーダーで数回しか起きないらしいということに気づきました。だから、小数点以下はなるべく沢山使う必要がある。
けれども、条件を変えると、そんなに桁数がいらない場合もある。それで、試行回数で増減させようとしたわけですわ。
プログラムにバグがありませんか?
「5個コミュニティがあって、4個が底抜け」の場合、「最初の4個が底抜けである確率」は1/5ですよね。英語版のターミナルで動かしてみたら、文字化けするんだけれど、なんか100%って出てくるようなんですが。
ちなみに、これはC++に対する挑戦だと考え、代わりに書いてみました。
配列でなく、コンテナを使うとこんなに短いコードになります。
画面表示の部分を除いたとしても、もう配列を使う時代ではないのですよ。
RubyやPythonでも良いらしいけど。
ソースでいえば
dig = dig.PadRight(Int(Math.Log10(rep)) + 3, “0”)
のあたりかな。
今回、ソースをアップするに当たって、「少なくとも sterai さんはソースを見るに違いない」と思っていたので、ちょっと緊張しました。
学生のとき、僕のソースを sterai さんが読んで、”event” のことを “ivent” と書いていたことをこっぴどくバカにされた恨みはいまだに忘れていません。
あ、問題間違えてた。「最初の9個の中に入る確率」を問題にしてたんですね。
失礼しました。
bmbさん:
「アタリ」の定義が違うのです。
僕にとって「アタリ」は、前から9個のスロットの中に全ての底抜けが入るかどうかです。
(完全に、mixi の世界を決め打ちしている)
だから、全体が5個だったら、絶対に9個のスロットの中に入るので 100% 「アタリ」です。
コンテナは VBちゃんでも使えるらしいのですが、不勉強で使いこなせません。
とりあえず、旧来の配列でゴリゴリやってできたので、ヨシとしました。
ついでに言うと、敢えてソースまでアップしておいたのは、bmbさんが釣られて revise するだろうことが容易に想像できたからです。しめしめ。
ちなみに、上のプログラムは「コミュニティリストの最初のx個が、底抜けで閉められる確率」を計算するものでした。
コンテナとか使うと、可視化できて楽ですよ。
あ、そうか、digはdigitの略か。納得。
風呂に入る前にシミュレーションの結果見て、風呂に入っている間に式を考えました。
steraiさんの言うように
{7C7 * (44-7)C2} / 44C9
これですね。順列とかいらないじゃんね。組合せだけで考えるべき問題だった。
こんなの間違えるようじゃ木公と僕は学位返上もんだぜ。
僕はちゃんとシミュレーションやって、文章まで書いたじゃないか。ちゃんと、先行研究=君らの意見もrefer してるぞ。立派なもんだ。
返すなら、ひとりで返してくれ。
bmb ソースを取ってきて、当blogサーバの C++ コンパイラにかけました。
「sokonuke.cpp:48:2: 警告: ファイル末尾に改行がありません」
とか言われました。
ちっ、と舌打ちしながら、ファイルの最後に改行を入れたらコンパイルが通りました。
よしよしと、”./a.out” してみたら、
「セグメンテーション違反です」
と、つれないメッセージで実行できませんでした。
c++ コマンドがダメなのかなぁと思い、違いはよくわかりませんが g++ を使ってみましたが、やっぱりセグメンテーション違反でした。
むーん。
g++ sokonuke.cppの後、
./a.out x y zです。
x=加入しているコミュニティの数
y=底抜けの数
z=レプリケーション回数
ちなみに、正確に書き直したらもっと短くなりました。
『プログラマの数学』(結城浩 ソフトバンクパブリッシング 2005年)、面白いよ。Amazonのレビューなんかだと、「理系・情報系の読者には読む価値なし」「文系の人たちにはいいんじゃないですか?」みたいな評価だけど、凄く奥が深い本だと思う。
ちなみに、「第5章 順列・組み合わせ」の「終わりの会話」は、
生徒「nやkなどが出てくると、難しいって思っちゃうんですが」
先生「まず5や3などの、小さな数で練習するのがよいですよ」
生徒「それだと、数が大きくなったときに、正しい結果になるか不安で……」
先生「だからnやkを使って一般化するんですよ」
p.s. iventの話全然おぼえてないです。でも、それ見つけちゃったら思いっきりからかうだろうなーと思う。ごめんねー。
bmbさん:
sokonuke-1.cpp 動きました。
こっちのプログラムで見ると、100万回に1回起きるかどうかですね。
実は、自分のプログラムで 100万回に3回とか6回とかは発生しすぎな気がしているわけですが、どこに違いがあるんだろう。
steraiさん:
結城浩って、本は読んだことないのですが、いろいろ調べものしていると web でよく引っかかる人ですよね。
「プログラマの数学」は、本当に読むかどうかはわかりませんが、頭の片隅にとどめておきます。
ivent の話のほかにもあって。
最初は自分のソースが他人に読まれることはないだろうと思ってコメントに愚痴を書いていたら、それも発見されて笑われた。僕にだけ言うならいいのに、みんなの前で暴露するんだもん。プンプン。
愚痴だけじゃないや。
コメントで、「うわっ。こんなロジックを考えるなんて、俺は天才!」とか、自分を励ますようなことも書いてて、それも逐一発見されたかもしらん。
>実は、自分のプログラムで 100万回に3回とか6回とかは発生しすぎな気がしているわけですが、どこに違いがあるんだろう。
それこそ、確率過程なのだから、分散がどれだけあるかという問題でしょう。
期待値だけでなく、次は、分散を計算してみたら?
VB6の時代の話だけど、シミュレーションやってて、どうも同じパターンが繰り返し現れているような気がして調べてみたら、「VB6のRND関数で生成される乱数系列は16777216個で一巡する」ということがわかりました。今のVBに仕様だとどうなっているんでしょうね?
なんの「期待値/分散」だろう。
処理系ごとの乱数発生関数の戻り値の分散の話になってきます?
今から考えると、16777216 = 2の24乗ですね。
VBの標準のライブラリよりも、「いくぶんマシ」といわれている乱数ライブラリを昔は知っていたような気がするのですが、今ブックマークを漁っても見つかりませんでした。
つーかさ、やっぱりコンピュータの擬似乱数には限界があるんだから、厳密にやろうと思ったら数式書いて解析するしかないんじゃないですか?
今回の問題も、計算機で解くんじゃなくて、紙と鉛筆の方がよっぽど厳密だってことで。
いやいや。Macで回しても100万回中5回のhitがでることもあるし、確率変数Xの平均M(X)だけでなく、分散Var(X)も求めないと、処理系にバイアスがあるか、そもそも計算が上手く行ってるか分からない、という話です。
>処理系にバイアスがあるか、そもそも計算が上手く行ってるか分からない
まったくそのとおりだと思います。
でも、分散も求めとかないとだめかなぁとは思ったのですが、もうコードが書くのがめんどくさかったので避けたという側面もあります。
コードのバグや計算間違いに関しては、今回は、(不完全ですが)わかりやすい条件設定でおかしなことが起きていないかチェックするのと同時に、ソースをレビューしてもらうという方法を取りました。
処理系のバイアスは、話のレイヤーが違って、問題があったとしても僕には手の出しようのない高度な話なので、無視するしかないかなぁ・・・と。
その幾分ましな乱数ライブラリ、以前木公に教えてもらったようなもらってないような……。でも、埋もれちゃって見つからないや。
そこで登場するのが、C++のBoostライブラリ。あと、任意精度の演算ならGMPライブラリ。1000桁でも1万桁でもメモリが許す限りの精度で数値計算できる。
けど、そこまでやっても、完全な数値計算は不可能なので、いつまで経っても数理モデルは消えない訳ですよ。
ついでなのでやってみましたよ。
コメントみないで、問題解いたけど、確かにp = 37C2/44C9ですね。この場合、100万回の試行における二項分布は(左から、成功数0,1,2,3,4,5)
0.390845195 0.367177236 0.172471082 0.054008876 0.012684543
上のプログラムで100万回の試行を200回やった時の成功数の分布は
0.31 0.42 0.15 0.10 0.02
高々200回なので、悪くはないですね。この手のシミュレーションとしては。
以上、逃避活動でした。
VBScriptでやってみました。時間がかかるので以下のプログラムでは繰り返し回数(nofrep)を10万回にしています(うちのマシンだとそれでも4秒くらいかかる)。
dim community(43)
dim histo(7)
dim nofrep
dim rep
dim drawing
dim sum
dim outputstring
dim r
dim i
randomize
for i = 0 to 7
histo(i) = 0
next
nofrep = 100000
rep = 0
do until rep = nofrep
rep = rep + 1
for i = 0 to 43
community(i) = 0
next
drawing = 0
do until drawing = 9
r = int(rnd * (43 + 1))
if community(r) = 0 then
community(r) = 1
drawing = drawing + 1
end if
loop
sum = 0
for i = 0 to 6
sum = sum + community(i)
next
histo(sum) = histo(sum) + 1
loop
outputstring = “”
for i = 0 to 7
outputstring = outputstring & i & “: ” & histo(i) & ” / ” & nofrep & ”
= ” & histo(i) / nofrep * 100 & “%” & vbnewline
next
msgbox(outputstring)
二千万回繰り返しても、1度も7つは揃わない。バグかも…。
do until drawing = 9
ではなくて
do until drawing = 7
for i=0 to 6
ではなくて
for i=0 to 8
かな。
for i = 0 to 6
sum = sum + community(i)
next
histo(sum) = histo(sum) + 1
ここ、0 to 8 じゃないんですか?これだと、「最初の7つのコミュニティに
底抜けが入っている数」を数えることになると思うんですが。
>do until drawing = 9
>ではなくて
>do until drawing = 7
do until drawing = 8じゃないの?
ランダムな位置に「底抜け」を割り振っている処理だと理解しています。
「底抜け」は7つなので、7回ループです。
#底抜けを1つ割り振るごとに、drawing をインクリメントしてるから、7ピッタリまで数える。
そっか。ここは7つの底抜けを43個の配列の中に割り振っているんだ。
木公クンとは全然違う作戦でプログラム書いてみようと思って、community(0~6)の7個が底抜けコミュ、community(7~43)の37個がその他のコミュ、最初全部0にしておいて、9個を選んで1を入れる。community(0~6)の合計が選ばれていた底抜けコミュの数、って作戦です。
sterai さんの考え方はわかりました。それを理解してソースを読むと、間違っていないように見える。
でも、確かに1回も7つ揃いが発生しない。
で、僕の書いた修正(あれはあれで、考え方としては間違っていないと思う)を施すと、100万回に1回くらいは成功する。
原因はなんなんだろうなぁ。
わかった。
sterai ロジックは、組合わせじゃなくて、”順列”を扱うことになってしまっているんだ。
草原→草々→小草若→・・・→若狭 という順序が守られて(順列)、7つ全部がトップにくる確率を求めてる。
そりゃ、順番はどうでもいいと考える場合(組合せ)に比べて、確率が低くなりますわ。1000万回行っても、たったの1回も発生しないかも。
bmb さんが、23:16:59 のコメントの時に考えていたことをプログラムに書き起こしてしまったんですよ。
いやぁ、変なところにいっぱい落とし穴があるね、シミュレーションって。怖い怖い。
気づいたきっかけは、
r = int(rnd * (43 + 1))
の部分を試しに
r = int(rnd * (9 + 1))
とかやってみた時。
50%の確率で7つ揃いが出ると判定されなければならないのに、sterai プログラムでは30%ほどしか発生しない。こりゃオカシイと思った。
これは本文でも書いたチェック法だけど、10個のコミュニティに参加してると仮定する方法。9個のスロットから外れるのは1つだけなので、底抜けが外れるか、採択されるかはちょうど50%となる。わかりやすくて確実な試金石。
↑あれ?ウソかも。
ちょっと混乱してきた。しばらく頭冷やす。
>で、僕の書いた修正(あれはあれで、考え方
>としては間違っていないと思う)を施すと、
>100万回に1回くらいは成功する。
というのは、
>do until drawing = 9
>ではなくて
>do until drawing = 7
>
>for i=0 to 6
>ではなくて
>for i=0 to 8
のことですか? でも、do until drawing = 7だと、44個から7個しか選んでないし、for i=0 to 8だとcommunity(7)とcommunity(8)の中身までチェックしてしまう(これらは底抜けコミュではないから調べなくてよい)。
それと、9つ選んだ「順序」はどこにも反映しないのだから、「順列」ではなく「組合せ」を数えていると思うのだけど…。
もう1回アイデアを説明すると、0~43番の郵便受けがあって、そこにランダムに9つの封筒を入れる(重複は許さない)。で、0~6番の郵便受けに入ってる封筒の数を数え上げる。どんな順番でどこに封筒を入れたかは問わない。あってるよねぇ?
郵便受けのメタファー、わかりました。
僕の頭の中では、こんなイメージがわいています。
具体的な人物(7人の弟子とか、山岸俊男とか山瀬まみとか・・・)が44人横一列に並んでる。空から天使が降りてきて、9つのメダル(重複を許さずに)を誰かの首にかけていく。ちりとてちんファミリー7人が全員メダルをもらうという状況ですね。
で、僕が11:10:07 に順列うんぬん言ったのも、おそらく誤りです。すみません。
相変わらず、なんで sterai プログラムだと1回もヒットしないのか、それはよくわかりません。
VBScriptのプログラムをExcelVBA上で実行すると実行時間が1/5程度で済むことがわかり、VBAプログラムとしていろいろ試してみました。その結果、やはり乱数の使い方(あるいは、乱数そのもの)に問題がありそうなことがわかりました。
例えば、
r = int(rnd * (43 + 1)) の一行上に
r = int(rnd) という乱数を無駄に1回発生させる行を付け足して、
r = int(rnd)
r = int(rnd * (43 + 1))
にします。すると、木公クンのプログラム同様、100万回の繰り返しで7回揃うのが0~3回になります。
これが乱数系列の問題なのか、乱数関係の関数の使い方がマズいのかの区別はつきません。ここでギブアップです。
後だしみたいで恥ずかしいけれど、rnd 関数の呼び出し回数は僕も気になってたんですよ。
まず、僕のプログラムと sterai さんのプログラムでは、rnd 関数を呼び出す回数が全く違う。
僕: 44回/試行
st: 9-11回/試行
そこで、僕がやったテストは、sterai プログラムで試行ごとに rnd を34回ムダに呼び出すというものでした。(発想はsteraiさんと同じ。ただし、呼び出した回数は僕の方が圧倒的に多い)
ところが、確か1回やってみて、ヒットが0回だったので「無駄足だった」と判断して、それ以上追及しませんでした。もしかしたら、偶々0回に当たっただけで、何回かやったらヒットしたのかも(確率的に十分あり得ることだ)。
あとで、調べられたら、もう一回やってみます。
上のほうで sterai さんが乱数系列のループの話を書いています。あの話を考慮すると、できるだけ乱数関数の使用回数は少ないほうがよさそうです。使用回数で比較すれば、僕のプログラムよりも sterai プログラムの方が圧倒的に少ないので、良いコードと言うことになる。
しかし、sterai プログラムの結果は、いまひとつ直感に合わない。
ますます泥沼ですねぇ。
ところで、郵便受けのメタファー。
sterai さんは、コミュニティを郵便受けに見立てて、トップに表示される権利を封筒に見立てている。封筒(権利)をランダムに配るというアイディア。
僕の考え方が、表示対象になる場所を郵便受けに見立て、「底抜け」コミュを封筒に見立てる。封筒(底抜け)をランダムに配って、表示対象となる郵便受けに入るかどうか。
どっちもありだと思う。
12:44:29 あたりでツッコミが入りましたが、僕の修正案は、コードはほぼそのままで 木公方式に変わるという風に説明すれば、OKですか?
#どっちのアプローチも少ない改変でカバーできるあたり、stプログラムを評価してる。結果が著しく変わるのはどーかと思うけど。
試しに、100万試行を200回でなく、1000回回してみた。
p = 37C2/44C9の二項分布
0.390845195 0.367177236 0.172471082 0.054008876 0.012684543 0.002383274
C++プログラムによる分布
0.384 0.366 0.178 0.054 0.017 0.001
プログラム(理論的に予測される)平均と分散
0.957 (0.9394433), 0.946 (0.9394424)
まぁ、こんなものでしょう。1万回ほど回せば、もっと理論的な分布に近づいていくはずです。
そう、逆転の発想。
実はVBScriptって昨晩初めて書いたんです。最初は全く木公方式と同じアイデアで、ところが! スワップのところで、
Community(i) = Community(r)
って書いたら、「型が違います」って何故かエラーになる。違ってねーよ!(怒)と、書きかけたプログラムを消しちゃって、その後このブログを見たら、この記事ができていたわけ。
で、VBScriptなんて、実行速度じゃVBにかなわないし、bmbさんのプログラムなんてハイレベル過ぎて何やってるのかさっぱりわからないし。
だったら、木公方式とは全然違うアイデアでやってみようと。ジョギングしながら、比較回数の少ない方法、スワップしないで済む方法(笑)を必死で考えた。
だけど、bmbさんのプログラムなんか見ると、「これが現代のプログラムってものなんだろうな~」と思うよね。俺のなんか、(悪い意味での)70年代テイストすら漂ってるよね。走りながら「いっそのこと行番号付きBASICプログラムにしたらウケるかな」なんて思いました。
ここまで読んだ。
木公くんのプログラム、やっと読んだけど、VBの関数の性じゃなくて、木公くんのせいだと思いますよ。
———————————-
For i = 1 To NofCom
r = Int(Rnd() * NofCom) + 1
sw = ar(i)
ar(i) = ar(r)
ar(r) = sw
Next
———————————-
この前で、「44個の配列の最初の7個を底抜けで埋める」ってやってるでしょう?
そのあと、このコードによって「最初の配列から順番に、(自分を含めた)ランダムな場所へ飛ばす」という作業をしている。
けど、これだと例えば「ar(3)からar(25)へ飛ばされた底抜け」が、さらに「ar(25)から別の場所へ飛ばされる」可能性が出てくる。一方、「ar(40)からar(10)へ飛ばされた」物は、その後、別の場所へ飛ばされる可能性が一切ない。
多分、マルコフ連鎖のようなモデルを書くと、遷移確率にバイアスが出てくるんだと思いますよ。多分、「44個の配列の一番最後の7個を底抜けで埋めてから、上のコードで乱打マイズする」と、今度は、「全く成功しない」試行数が増えるんじゃないかな。
実は、bmbさんのプログラム結果の見方がわからないのだけど、そもそもの「mixiのコミュニティ一覧(コミュ9個)に底抜けコミュ7つが全部表示される確率」の値はいくらだということになるのですか?
C++プログラムによる分布
0.384 0.366 0.178 0.054 0.017 0.001
左から「100万回の試行中、底抜けが0(1、2、3、4、5)回出てきた回数/1000」です。
分かりにくいな。
「100万回の施工中、7つの底抜け全てが、最初の9個の枠の中にそろった回数が、0(1、2、3、4、5)だった回数/1000」です。
お、と言うことは、そもそも「7回出てきた回数(確率)」は出てないわけね。どうりで見方がわからなかったはずだ。
ただ、素朴な疑問なんだけど、何で、p = 37C2/44C9の二項確率を求めてるんだろう?
9個の枠の中に底抜けコミュが
0個表示される確率 = 7C0 * 37C9 / 44C9
1個表示される確率 = 7C1 * 37C8 / 44C9
2個表示される確率 = 7C2 * 37C7 / 44C9
3個表示される確率 = 7C3 * 37C6 / 44C9
4個表示される確率 = 7C4 * 37C5 / 44C9
5個表示される確率 = 7C5 * 37C4 / 44C9
6個表示される確率 = 7C6 * 37C3 / 44C9
7個表示される確率 = 7C7 * 37C2 / 44C9
じゃないのかな?
あ、ごめん。17:32:10のやつ見ないで、17:38:22のやつを書いちゃった。
たぶん言ってることわかった(と思う)。
> 一方、「ar(40)からar(10)へ飛ばされた」物は、その後、別の場所へ飛ばされる可能性が一切ない。
一切無いわけではありません。
例えば、ar(41)の入れ替え先が、たまたま ar(10)になるかもしれない。
配列のランダマイズの方法としては、ポピュラーだと信じてるんだけどなぁ。僕のバイブルの奥村晴彦『C言語による 最新 アルゴリズム事典』の「ランダムな順列」という項にも載ってるし。
僕が正しく vb に移植したかどうかは定かではないケド。この本も「最新」と銘打ってる割には15年くらい前の本だケド。マルコフ連鎖という文字列は見慣れてるけど、概念はさっぱりわかってないケド。
>一切無いわけではありません。
例えば、ar(41)の入れ替え先が、たまたま ar(10)になるかもしれない。
けど、飛ばされた先から、さらに飛ばされることはないのでしょう?
「1回だけ飛ばされる回数」は、配列の後ろほど高くなり、「2回以上飛ばされる確率」は配列の最初ほど高い。
ここが問題じゃないかと言う話です。試しに、上に書いたように「44個の配列の最後の7個を底抜けで埋めてから、ランダマイズ」してみたら?それで、結果が変わらなければ、何か別の原因があるという話になるのだから。
困ったときのグーグル。
http://ray.sakura.ne.jp/tips/shaffle.html ー 余談を参照
http://blade.nagaokaut.ac.jp/cgi-bin/scat.rb/ruby/ruby-list/41356
バイブルから移す時、書き間違えてない?
id: 83283の bmb さんの指摘を読んで、とりあえずシャッフルモジュールだけ抜き出してゴリゴリまわしてみた。
ちょっと笑えることになった。
今、画像とか準備してる。
その次のコメント(id: 83284)のURLはチラッと眺めたけれど、まだ吟味してない。
100個の配列に、0~99の数字を1つずつ代入。
For i = 1 To 100
r = Int(Rnd() * 100 + 1)
sw = ar(i)
ar(i) = ar(r)
ar(r) = sw
Next
というコードでシャッフル。
約87,000回行った(そこで、シビれをきらせた)。
各配列要素ごとに、代入されている数値の平均値を求めた。もし均等にシャッフルされてるなら、どの要素の平均値もおよそ49.5くらいになるはず。
では、グラフをご覧下さい。
見返り美人の瓜実顔を髣髴とさせる、美しい曲線だねぇ。
何かがおかしい・・・。
さて、僕のシミュレーションプログラムで、コメントid:83283のご指摘どおり、「底抜け」の初期配置を配列の後ろ側において実行しました。
100万回の試行を3セットやって、7つ並ぶケースは0でした。本当はもっとやった方が良いのだけれど、元のプログラムでは3回やったら少なくとも2回はhitするので、明らかに結果が違うと思って打ち切った。
r = Int(Rnd() * 100 + 1)
を
r = Int(Rnd() * (i-1))
に変更すると、瓜実でなくのっぺりとした平たい面長な顔が出てくるはずです。
確かに、妖怪ぬりかべのようなのっぺりしたヤツが現れそうなデータになりました(もうめんどくさいから、グラフは書かない。平均値の数列を見て一目瞭然だったし)。
で、確かに、バイブル(奥村著『アルゴリズム事典』)をよーく見直したら、rnd 関数周りの扱いを間違えていました。
冷や汗ものですな。15年近く、ずーっと間違って覚えてた。
#僕が作ったプログラム等を鵜呑みにして、シャッフルの部分を書き換えなかった諸君、全員アウトです。;-p
悔しいから、いたちの最後っ屁をしておくと、
> r = Int(Rnd() * (i-1))
は、上のプログラムに当てはめるなら
r = Int(Rnd() * (i-1) + 1)
だよね、きっと。
僕のシミュレーションプログラムは、シャッフル部分がおかしくて、かなり高確率になっていたようです。
シャッフル部分を直したら、1千万回に2回くらいに落ちました。
さてさて、また sterai プログラムとの比較が気になるのですが、彼のやつだと2千万回まわしてもhitしないんですよねぇ。なんでだ~。
でも、僕もそろそろ考える気力がなくなってきた。
コメント数も既に60を超えてるし。いまだかつてこんなのねーよ。
おかげで、コメントIDというリンクを急遽作っちまったじゃねーか。コメントごとのURLを取れるから、適当にアンカータグ()で埋め込んで使える。
・・・で何回か自分で使ってみたけれど、あんまり便利じゃないね。
そのうち、人知れず消えるかも。
Basicのループとか細かい点は忘れたけれど、ともかく「自身を含む下位の配列の中からランダムに位置を決める」ということですね。
という訳で、「古典的で基礎的な関数のみを持つ言語で、何でもガリガリと基礎から書き上げる」より、「数学的に妥当性が保証されたライブラリを備えたモダンな言語」の方が、リスクは少ないという話です。人間、ロジックを理解する事はできても、実際にimplementするときにエラーを起こしてしまう存在だから。
C++のプログラムでは、[0,1,2,…43]という配列を作って、これをrandom_shuffleという関数でシャッフルし、「最初の9つの中に0~7の全てが入っているか」を判定しています。基本的に、random_shuffleがやっているのは奥村と同じアルゴリズムらしいけど。
「数学的に妥当性が保証されたライブラリを備えたモダンな言語」を自分で使うよりも、「自分よりも頭の良いヤツに計算してもらう」方がさらにリスクが小さくないですか?;-p
それがこのエントリの最初の趣旨だったのに、いつの間にか自分でドップリと手を動かしてしまいましたよ。
とは言え、信頼の置けるライブラリを使うのが better というのは同意です。
会社で隣の席のメキシコ人(知性の塊)が「FORTRAN 以外は危なくって使えない」みたいな事を言ってました。彼に言わせると、CもMatlabもダメダメだそうです。
なお、彼が本当に頭がいいと思った瞬間は、音声周波数の概念についてイロハを教えてもらった時。日本人の誰から教わるよりも、彼の完璧ではない日本語で教わった方がよく理解できた。
このネタはalm-ore的にどんぴしゃりだったわけね。コメント数69って、みんな盛り上がりすぎだろ。こっちがエディタ立ち上げる前にみんなプログラムアップしてるんだもん。
blog 全体のコメント数が3,500件くらい。
ここには、一昼夜で70件のコメントが付いたから、実に2%に相当。
このblogが開設されてから、およそ1600日。
blog の歴史の0.06%の時間で2%のコメントが付いたんだからすごい。
>こっちがエディタ立ち上げる前にみんなプログラムアップしてるんだもん。
そうなんだよ。エキサイティングだったねぇ。
おっと、寝てました。
件のシャッフルのアルゴリズムだけど、僕もずっと木公方式で書いてたよ。Quick BASIC時代から。って言うか、初めての学会発表とか、学会誌にまで、例のアルゴリズムで書いたシミュレーション結果で論文発表しちゃったよ…。
最初はsteraiさんのVB scriptの方式でやってましたね。まだ値がアサインされてないセルからランダムに探す方式。
>で、確かに、バイブル(奥村著『アルゴリズム
>事典』)をよーく見直したら、rnd 関数周りの
>扱いを間違えていました。
念のため、書き写して貰えませんか?
ちなみに、僕が木公方式(って言うか、もちろん木公クンと知り合う前からこのやり方をつかっていたわけだけど)のランダマイズのやり方をおぼえたのは、元をただせば山岸先生のシミュレーションプログラムだったんじゃないかなぁ…。生涯僕の書いたプログラムでは全部でこの方式を使っている。って言うか、他人にまでこのやり方を随分広めちゃったよ…。
奥村先生の本は、会社に置きっぱなしです。月曜日まで待っていただけますか?
頭の中におよそ入っているのだけれど、いいかげんなことを書いてこれ以上ノイズを増やすのもどうかと思うので、やめときます(ループを n で始めるのか n-1 で始めるのかとか、細かいところがやばい)。
なお、事典での見出しは「ランダムな順列」。これは間違いない。ぐぐれば、月曜日前に見つかるかも。
#今、ちらっと見た限り、そのものズバリは見つからなかった。
前にもリンクしたけど、ここの最後の奴だと思いますよ。
http://ray.sakura.ne.jp/tips/shaffle.html
奥村本に出てたのは「改善策」の1つ目の方だと思いますです。
失礼。STLのrandom_shuffleのほうだった。
>なみに、僕が木公方式(って言うか、もちろん木公クンと知り合う前からこのやり方をつかっていたわけだけど)のランダマイズのやり方をおぼえたのは、
まぁ、どこでどう使っているかによりますよね。ランダマイズした後で、配列の頭と後ろのどちらに来やすいかに意味があるなら(e.g., 今回の底抜けシミュレーションなど)まずいけど。それよりも、rand関数自体のゆがみも大きいから、実験などで数十回呼び出すくらいなら、大丈夫ジャマイカ。
僕もそう思う。
ありがとうございます。
今、ジワジワと怖ろしさを感じ始めてきたのだけど、本当に僕、ありとあらゆるプログラムでこの方式でランダマイズしていたので、「実験参加者を複数の条件にランダムに割り振る」とか、「参加者同士の組合せをランダマイズする」とか、全部このやり方でやってたんですよ。ランダムアサインしてなかったのか~と。「ちゃんとランダムアサインになってるかどうか」を調べたこともなかった。「青信号は『進め』」だと思い込んでた、みたいな話(実際は「青信号は『進むことができる』」)。しかも、僕、他人の実験プログラムにまで手を入れたりしてたでしょう。やばいなぁ~。
おっと、また時間差攻撃を喰らった。
実は、最後のシャッフルの議論、まだ正確に理解していないんだけど、要するにこれって、「くじを先に引いた方が有利か、後に引いた方が有利か」(もちろん「有利さに差はない」が正しい)というのと同じ話なんですよね? この3時間、樹形図描きまくって、前のシャッフルのやり方がまずかったのは、「先にくじを引いて確定したはずの結果を、後の人がくじを引いた時点で覆している」ということなのだろう、とようやくわかってきました。これは面白いので、ちゃんと理解できたら、僕も自分のブログに書いてみようと思います。
ごめんなさい、上の話違うわ(関係はしているのかもしれないけど)。前のシャッフルの仕方が何故ダメかというと、上記リンク先にも書いてある通り、「並び方」のパターン数がn!なのに、「並び替え方」のパターン数がn^nなので、「並び方」の各パターンの生起頻度に偏りが生じてしまう、ということなのですね。
すっかり忘れるところでしたが、奥村本の記述に関するメモを sterai さんにメールで送りました。
#参考URLも挙がってから、用済みかもしれんけど。
他にも欲しい人がいたらメールで連絡ください。
こちらこそ、すっかり忘れていました(笑)。ありがとうございます。
もう随分経ちましたが…、最近C#を始めたので、半年前にVBScriptやVBAで書いたプログラムをC#で書きなおしてみました。1000万試行が4~5秒で終わるのでビックリしました(VBScriptだと10万試行で4~5秒かかった。その差100倍!)。
前は2000万回繰り返しても7つの底抜けコミュ全部が揃うことが一度もなくて、最終的に乱数の問題か乱数の使い方の問題だろうと考えたんですが、今回は1000万回の繰り返しで(正しく)5~13回ほど7つ全部が揃います。やっぱり、乱数関係の問題なんですかね。
ちなみにプログラムはこんな感じです。相変わらず「手続き指向」です。
const int nRep = 10000000;
const int nCommunity = 44;
const int nSokonuke = 7;
const int nAtari = 9;
int[] community = new int[nCommunity];
int[] histogram = { 0, 0, 0, 0, 0, 0, 0, 0 };
Random rnd = new Random();
for (int rep = 0; rep
あれ? プログラムをコピー&ペーストしたはずなんだけど、一部おかしくなっている(8行目のforのところ)。
for (int rep = 0; rep for (int i = 0; i community[i] = 0;
じゃなくて、
for (int rep = 0; rep
あれ? やっぱりおかしくなってる…。
< とかの記号がHTMLタグとして認識されてしまっているのかも。
メールでソースを送ってくれたら、ちゃんと見えるように修正しておきますよ。
あ、なるほど…。forの継続条件の「i < ○○」なんかのところでおかしくなってます。
それどころか、whileの継続条件も消えちゃってて、無限ループになってますね!